Recentemente contemplado pelo edital de jovens pesquisadores da Fapesp e pelo edital de mobilidade do Santander, tornando possível a realização do aprofundamento de sua pesquisa na Universidade de Exeter, na Inglaterra, Pedro da Silva Peixoto, professor do Instituto de Matemática e Estatística da Universidade de São Paulo (IME-USP) e especialista em dinâmica de fluidos geofísicos na esfera, está trabalhando com novos modelos de previsão do tempo por meio do aprimoramento dos cálculos matemáticos envolvidos no processo. Entre as linhas de desenvolvimento de Peixoto estão a resolução das instabilidades artificiais geradas na previsão do tempo por conta do modelo matemático aplicado e formas de resolução de imprecisões da malha de segmentação do globo terrestre.
Modelos clássicos de previsão do tempo usam a divisão do globo em latitudes e longitudes. Esse modelo, entretanto, possui um problema na região dos Polos, já que a convergência de linhas torna a eficiência de supercomputadores muito lenta, gastando tempo excessivo em uma região que a condição atmosférica é praticamente estável e dando pouca precisão à previsão na Linha do Equador, já que, quanto menor a área delimitada por cada célula na malha, mais precisa a previsão. “O modelo de malha com que trabalho, por outro lado, se assemelha a uma bola de futebol e evita esse tipo de problema, fazendo uso mais eficiente dos supercomputadores modernos”, explica Peixoto.

A nova malha, que faz parte do Next Generation de modelos de previsão do tempo, apesar de ter resolvido o problema dos polos, ainda possui alguns desafios a serem solucionados por Peixoto e outros estudiosos do modelo. Um desses enigmas é o fato de que esse tipo de malha acaba gerando inconsistências matemáticas na resolução dos cálculos necessários para prever o movimento das ondas atmosféricas. “Toda previsão do tempo é resultado de uma série de análises, entre elas, a resolução de equações matemáticas. Essas equações não possuem resultados exatos e a aproximação gera, em alguns pontos do globo, algumas instabilidades climáticas irreais. É como se, por conta do cálculo, chovesse mais em determinado ponto. Analisando as condições reais, aquela situação climática não existe, mas é apontada pelo modelo matemático”, expõe o professor.
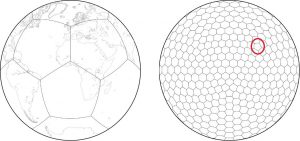
Outro problema que o professor aponta é a aparição de deformidades na malha. É impossível recobrir a superfície do globo somente com hexágonos e a aparição de pentágonos torna a malha disforme, complicando a resolução das equações matemáticas e, consequentemente, a realização de uma previsão do tempo precisa. “Visualizar uma malha sobreposta e não uma representação perfeita do globo terrestre é um dos grandes problemas de imprecisão que precisam ser solucionados por meio de artifícios matemáticos. Uma das constatações de anos de pesquisa é que não existe modelo de previsão do tempo perfeito e toda solução vem com mais um contratempo que a matemática se propõe a resolver”.




Faça um comentário